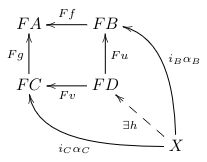
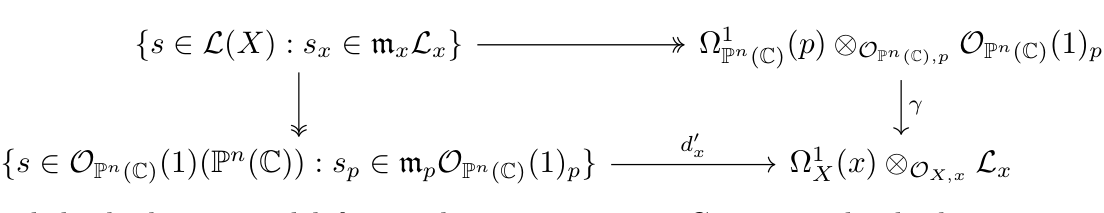Writing | Areeb SM's website

Unpublished

Preprint

2025

Empirical Measures and Strong Laws of Large Numbers in Categorical Probability

Tobias Fritz, Tomáš Gonda, Antonio Lorenzin, Paolo Perrone, and Areeb Shah Mohammed

Mar 2025

Abs DOI arXiv

The Glivenko-Cantelli theorem is a uniform version of the strong law of large numbers. It states that for every IID sequence of random variables, the empirical measure converges to the underlying distribution (in the sense of uniform convergence of the CDF). In this work, we provide tools to study such limits of empirical measures in categorical probability. We propose two axioms, permutation invariance and empirical adequacy, that a morphism of type $X^\mathbb N \to X$ should satisfy to be interpretable as taking an infinite sequence as input and producing a sample from its empirical measure as output. Since not all sequences have a well-defined empirical measure, "such empirical sampling morphisms" live in quasi-Markov categories, which, unlike Markov categories, allow partial morphisms. Given an empirical sampling morphism and a few other properties, we prove representability as well as abstract versions of the de Finetti theorem, the Glivenko-Cantelli theorem and the strong law of large numbers. We provide several concrete constructions of empirical sampling morphisms as partially defined Markov kernels on standard Borel spaces. Instantiating our abstract results then recovers the standard Glivenko-Cantelli theorem and the strong law of large numbers for random variables with finite first moment. Our work thus provides a joint proof of these two theorems in conjunction with the de Finetti theorem from first principles.

2024

Hidden Markov Models and the Bayes Filter in Categorical Probability

Tobias Fritz, Andreas Klingler, Drew McNeely, Areeb Shah-Mohammed, and Yuwen Wang

Jan 2024

Abs DOI arXiv Code

We use Markov categories to develop generalizations of the theory of Markov chains and hidden Markov models in an abstract setting. This comprises characterizations of hidden Markov models in terms of local and global conditional independences as well as existing algorithms for Bayesian filtering and smoothing applicable in all Markov categories with conditionals. We show that these algorithms specialize to existing ones such as the Kalman filter, forward-backward algorithm, and the Rauch-Tung-Striebel smoother when instantiated in appropriate Markov categories. Under slightly stronger assumptions, we also prove that the sequence of outputs of the Bayes filter is itself a Markov chain with a concrete formula for its transition maps. There are two main features of this categorical framework. The first is its generality, as it can be used in any Markov category with conditionals. In particular, it provides a systematic unified account of hidden Markov models and algorithms for filtering and smoothing in discrete probability, Gaussian probability, measure-theoretic probability, possibilistic nondeterminism and others at the same time. The second feature is the intuitive visual representation of information flow in these algorithms in terms of string diagrams.

Technical Reports

Expository

2023

Introduction to Equivalences of Categories

Areeb Shah Mohammed

Mar 2023

Prepared for a student seminar on Noncommutative Geometry

Abs PDF Slides

These are notes for a student seminar talk I did as prerequisites for noncommutative geometry. Purely expository, but I’m leaving them here in case they are of interest to anyone. Of course, all errors are due to me and me alone ;) As for the contents, it doesn’t really have very much to do with noncommutative geometry in particular. It’s mostly an introduction to anti-equivalences, since most noncommutative geometrical objects are anti-equivalent to corresponding noncommutative algebraic objects.

2022

The Mitchell-Bénabou Language

Areeb Shah Mohammed

Jun 2022

Prepared for a master’s degree seminar on Topoi, Logic and Forcing

Abs PDF

These are notes for a student seminar talk I did during my master degree. Purely expository, but I’m leaving them here in case they are of interest to anyone. Of course, all errors are due to me and me alone ;) As for the contents, the notes start by recalling what it means to interpret first order logic in a Heyting category. They then discuss how the tautological structure of a topos extends this to two variants of the Mitchell-Bénabou language. It ends by presenting a Kripke-style semantics for the Mitchell-Bénabou language.
Resolutions, Homology and Cohomology

Areeb Shah Mohammed

Jul 2022

Prepared for a master’s degree seminar on Model Categories

Abs PDF

This is a report for a student seminar talk I did during my master degree. Purely expository, but I’m leaving it here in case it’s of interest to anyone. Of course, all errors are due to me and me alone ;) It’s one of the shorter ones, as this seminar had a limit on how long the reports could be :P. It starts with a discussion of Quillen homology, reviews a few examples, and goes on to discuss resolution model categories.

2021

Homology, Cohomology and Products

Areeb Shah Mohammed

Jul 2021

Prepared for a master’s degree seminar on Stable Homotopy Theory

Abs PDF

These are notes for a student seminar talk I did during my master degree. Purely expository, but I’m leaving them here in case they are of interest to anyone. Of course, all errors are due to me and me alone ;) As for the contents, the notes start by discussing the homology and cohomology theories induced by spectra. It is sketched how all (co)homology theories are conversely presented by spectra. The rest of the notes discus the various products (exterior, slant, cup, and cap) induced on these theories.
Projective Embeddings and Abelian Functions

Areeb Shah Mohammed

Jul 2021

Prepared for a master’s degree seminar on Theta Functions, Complex Abelian Varieties and Moduli Spaces.

Abs PDF

These are notes for a student seminar talk I did during my master degree. Purely expository, but I’m leaving them here in case they are of interest to anyone. Of course, all errors are due to me and me alone ;) As for the contents, the notes start by discussing a standard technique for constructing projective embeddings of a complex torus (with a recollection of what that means). The case of Polarized Abelian Varieties is then specialized to. An actual projective embedding is then constructed, and the notes move on to describe a characterization of the ring of abelian functions. The final section is an identification of the Picard group of an abelian variety using Appell-Humbert data.
Projective Embeddings of Compact Riemann Surfaces

Areeb Shah Mohammed

Jul 2021

Prepared for a master’s degree course on Sheaf Cohomology

Abs PDF

This is a short note for a course I had during my master degree. Purely expository, but I’m leaving them here in case they are of interest to anyone. Of course, all errors are due to me and me alone ;) As for the contents, the notes start by discussing a characterization of projective embeddings. Embeddings for compact Riemann surfaces are then demonstrated by the identification of very ample line bundles.

2019

The Freyd-Heller group and the failure of Brown representability

Areeb Shah Mohammed

2019

Prepared for the University of Chicago Mathematics REU

Abs HTML

It is a classical result due to Edgar Brown that any set valued contravariant functor on the homotopy category of connected based topological spaces taking coproducts to products and weak pushouts to weak pullbacks is representable. This is however, false when we drop the assumption that our spaces and maps are based, or if we drop the assumption that the spaces under consideration are connected. We describe a construction, often called the “Freyd-Heller” group, that results in a counterexample in both cases.

Theses

Masterarbeit

2022

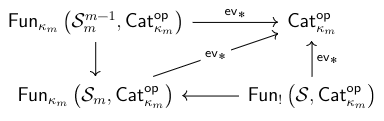On a characterization of Higher Semiadditivity

Areeb Shah Mohammed

Universität Regensburg, Nov 2022

Survey article: all results are generally already known. Contains a few alternate proofs in an attempt to work as much as possible with quasicategories as opposed to simplicial categories or complete Segal spaces.

Abs PDF

Michael Hopkins and Jacob Lurie have introduced for $m\ge -2$, a notion of m-semiadditivity. This generalizes the classical notion of a semiadditive (infinity) category. Intuitively, m-semiadditive infinity categories are those in which limits and colimits of diagrams indexed by m-finite spaces (that is, m-finite infinity groupoids) are canonically equivalent. Yonatan Harpaz proves a universal property of the infinity category of spans of n-finite spaces with m-truncated wrong way maps. This is used to establish an equivalent characterization of m-semiadditivity in terms of a well behaved, essentially unique action of this category of spans. This approach has the advantage of not only providing a more succinct method of detecting m-semiadditivity, but also providing a versatile structure to work with m-semiadditive infinity categories. In this thesis, we survey this sequence of results.